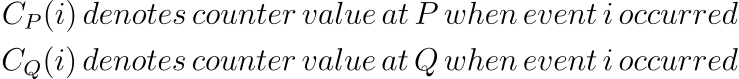Paper Pursuit #4 - Time, Clocks, and the Ordering of Events in a Distributed System
Author: Leslie Lamport [1978]
Original paper: Time, Clocks, and the Ordering of Events in a Distributed System
Introduction
Time, Clocks, and the Ordering of Events in a Distributed System by Leslie Lamport is an important piece of work that introduces the concept of logical clocks to achieve synchrony in a distributed system.
The concept of “happened before”
Time in a distributed system is not as straightforward as one might think. Before I dive into the paper, let me introduce a distributed system. The paper succinctly defines it as a system that is made up of spatially separated processes. This spatial separation introduces two interesting scenarios:
The concept of absolute time is skewed
Communication from one process to another includes a time delay
These two properties make the study of time and ordering an important part of operating distributed systems. Let’s take an example to understand why this is crucial and what may go wrong if order is not taken into consideration.
Let’s consider computers use the time of the day (timestamps) to compare which event happened first. Consider Ben (our hypothetical subject) wants to buy a t-shirt that he likes a lot from a fashion e-commerce website, but he isn’t earning yet so he asks his sister Lily to send him some funds to his bank account so that he can finally buy his favorite graphic tee. There is a hot drop sale that will last for a few minutes before stocks wipe off the website, Ben has to be quick.
Ben is an impatient teen and cannot wait so he proceeds to place an order, expecting Lily to have transferred the funds. Lily, has in fact transferred the funds, there is a caveat though — Lily’s computer has a clock that is running 1 minute ahead of the actual time. When she transfers the funds, the bank notes the time as 18:30:35 (hh:mm:ss) circa 18:29:35 in actual time.
Now the fashion e-commerce website initiates the payment request to Ben’s bank account. This is done on a server that is synced perfectly with the Internet time and the time noted by this server is 18:30:00.
When the bank server receives these two requests, it sees that the fund transfer was done at 18:30:35 and the purchase request came in at 18:30:00 and hence processes the purchase first. The purchase fails because Ben does not have enough funds in his account. Uh oh! Poor Ben cannot get his favorite tee.
This is a very simple scenario, but you can imagine other similar ones in the scope of distributed systems. Determining if an event happened before the other is a tricky affair and depending only on timestamps is not a great idea as they may not be synced correctly across processes.
Partial Ordering of Events
Before tackling the problem of time and the overall ordering of events, the paper talks about the partial ordering of events. Partial ordering is, given two events a and b, stating which event happened before the other. Lamport introduces the relation
a → b as a happened before b
This relation also means that
if a -/→ b and b -/→ a, then a and b are concurrent. (-/→ is “did not happen before”)
Causality
Causality is the property of one event affecting the other. a and b have a causal relationship if a affects in some way the occurrence of b (e.g. a triggers b). In this case,
a → b has to be true.
This is because b happens because a happened before.
If two events are not causally related, they are concurrent. This is because there is no way to compare their occurrence in time.
Logical Clocks
The paper then introduces logical clocks — these are located at each process and they hold a counter value that is incremented between consecutive events in a process. Two processes P and Q holding the clock values for an event i can be denoted as follows:
While sending messages, a process sends the counter value (as a timestamp for an event) along with the event. The receiving process can read this value.
For two events a and b (a happens in P and b happens in Q):
This constraint introduced by the logical clocks is important to partially order events occurring in different processes. Now, in order to respect this constraint:
Each process increments its counter value C between any two successive local events
If P sending a message to Q is event i at C(i) and Q receiving the message is event j at C(j), then Q must set C(j) to a higher value than C(i).
These two conditions ensure that the processes maintain the correct ordering of events using the logical clock counters, and hence partial ordering is achieved.

The figure above shows an example of how two processes maintain the constraint to make it possible to determine the partial ordering of two events.
Total Ordering
In order to determine the global ordering of events in a distributed system, we must be able to relate events across all processes. To do that, we define a new relation of total ordering ⇒. If a is an event in process P and b is an event in process Q, then
a ⇒ b if and only if either C(a) < C(b) or (C(a) = C(j) and P < Q)
P < Q is any arbitrary ordering for processes.
Example
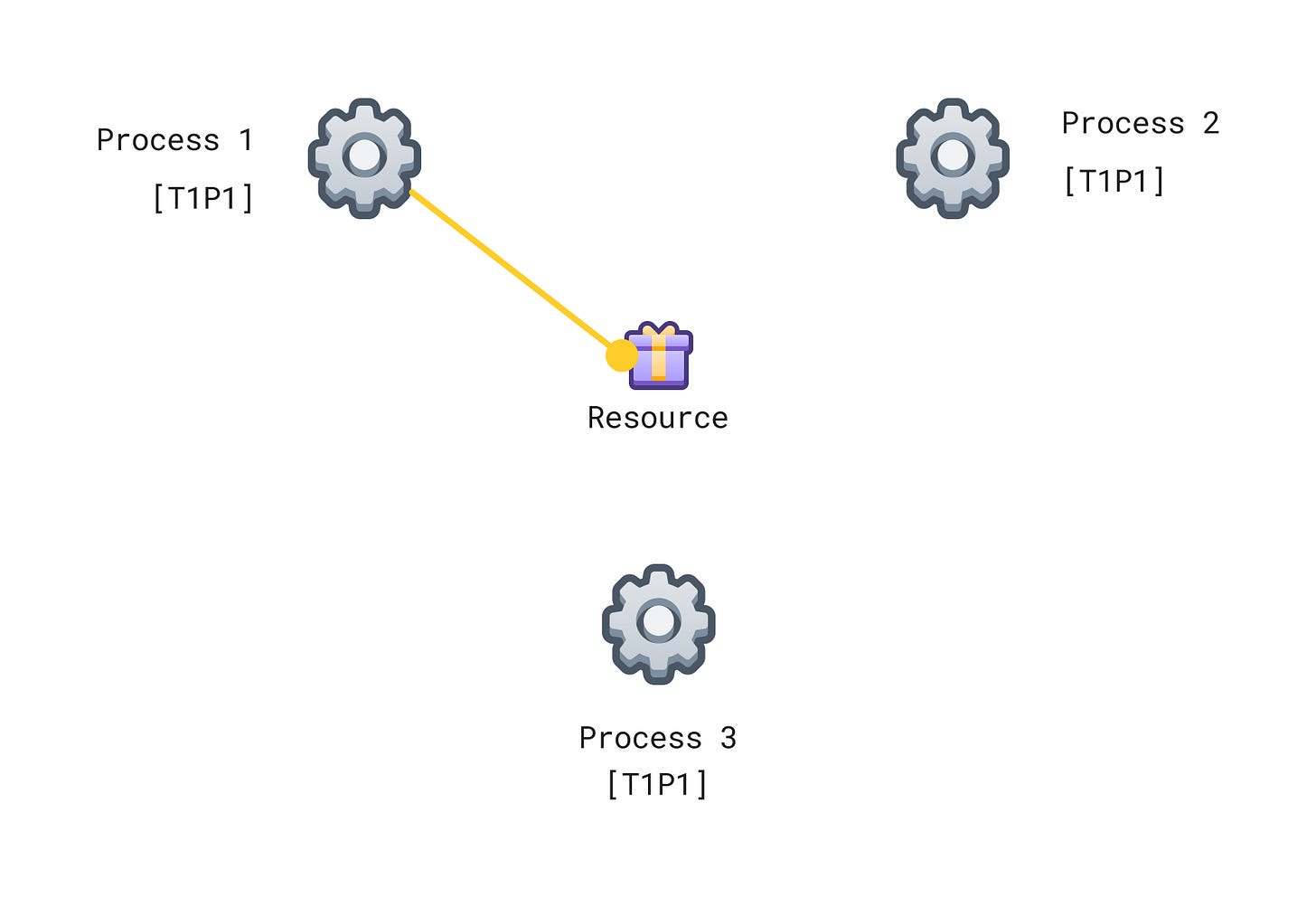
The paper describes an example of a system where multiple processes share a single resource. A central scheduler process is not possible as it introduces the same challenges as described earlier when using only timestamps. The system should respect first-come-first-serve for the single resource as it can only be accessed by one process at a time.
We will use a system of logical clocks as described above to totally order events happening in the system and decide which process gets the resource. The following diagram shows the setup.
Each process maintains its own request events queue. Each process that wants to access the resource will send a request event (with a timestamp) to all other processes. Initially, we will assume that a process has access to the resource, hence all processes will have T1P1 (assuming P1 requested at time T1) in their request queues as shown in the diagram.
The system works as follows:
To request access to the resource, a process Pi sends a message of the form TxPi. Here Tx is the timestamp of the request event.
When the other process Pj receives TxPi, it adds it to its request queue.
To release the resource, Pi removes any TxPi request message from its request queue and sends a timestamped release resource message to all other processes. Each other process removes any TxPi from their queues.
A process Pi is granted the resources when both conditions are true:
There is a TxPi request message in its queue before all other request messages (determined by total ordering).
Pi has received a message from every other process timestamped later than Tx.

That works great! This algorithm using logical clocks solves our problem of asynchrony between processes. Every event happening after another event is guaranteed to have a larger counter value.
But there is a caveat. The system above uses total ordering for picking which event happened before and has no context of real-world time. Assume a situation where P1 is a computer owned by a person in Berlin who makes the request for the resource over the Internet and then calls up their friend in Mumbai who has a computer P3 to make a request for the same resource. If the Internet was totally ordered using logical clocks, there is a high chance that P3’s request would get a lower counter value than P1’s. This is because there is no relation to real-world time while assigning counter values.
Using Physical Clocks Instead
The anomaly mentioned above can be solved by replacing the logical clocks in our solution with synchronized physical clocks. This means that the counter value for each process is an actual timestamp (e.g. UTC epoch). The rest of the logic stays the same — when a process receives an event, it sets the event’s timestamp as the maximum of its own timestamp and the one received with the event.
The paper then discusses the reliability of physical clocks as it is inevitable to avoid them from going out of sync with actual time. Today, computers use the Network Time Protocol to keep their clocks closely in sync with UTC, keeping the deviation under a few milliseconds.
The paper concludes by providing mathematical proof of how closely physical clocks can be synchronized. The solution of total ordering in combination with physical clocks is proposed as a solution to achieve synchrony in a distributed system.
Takeaways and further readings
The concept of time is interesting in the field of distributed systems and a lot of research has been done in this area. This paper was a seminal contribution to the field. Leslie Lamport’s other impactful contributions include LaTex, the popular typesetting system.
Following are some resources you can explore:
Distributed Systems Lecture Series, Martin Kleppmann
Did you enjoy today’s issue? You can share it with someone you know who would be interested in reading! Sharing also supports my newsletter by increasing its reach and letting more people know about my work. So send this post around! 💛 I’ll see you next Tuesday.